|
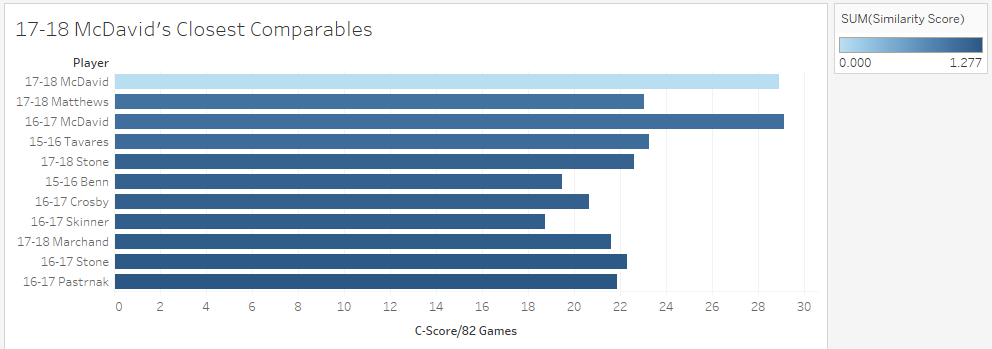
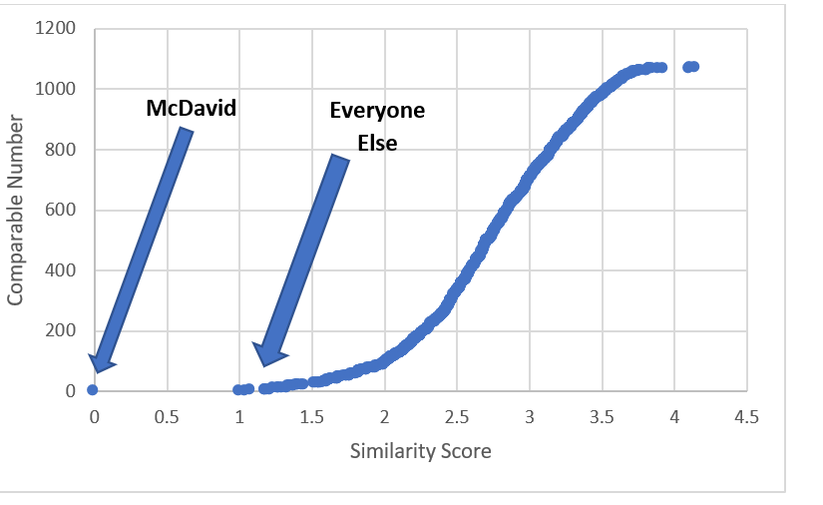
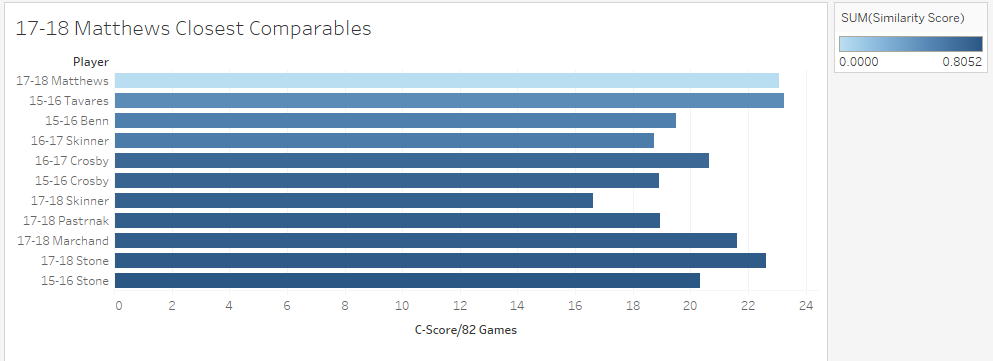
Just like Sidney Crosby was for a long time, Connor McDavid is significantly better than anyone else in the world at hockey. This could be true for like a decade, and will probably get boring. Que talking heads on T.V, or someone looking for a hot take on twitter to say how someone is actually close to the best player on earth. It happened with Toews for Crosby, and yesterday it erupted about Matthews and McDavid. This left me wondering, who is Connor McDavid's best comparable? To answer this I used my new metric, C-Score. I don't have a write-up yet, but think of it like a greatly improved version of my old GAR (So much so everytime I say C-Score you may just want to think GAR). It tries to take all of a players important stats, and boil their output down into one number. There is a small ex-plainer on the C-Score sheet, and I can help answer questions about it on twitter or in the comments. From C-Score the goal was to find a similarity rating for each player. To do this I started with creating a Z-score for each input into overall C-Score. This measures how many standard deviations away from the mean a player is at each component of the game. This is a great way to compare skills across different years. With those Z-Scores you can easily see how close certain players are in each skill. From there I took the absolute value of the sum of the differences in Z-Scores, and weighted them by how much each metric is worth overall. So for example, BPM, which represents weighted counting stats at 5v5, is worth far more to a players C-Score than Face-offs, so, having a similar BPM rating means way more to the overall similarity score than having a similar face-off rating. With that, It's time to look at Connor McDavid's comparable seasons from the past 3 years, meaning I'm talking recent history for this post. Connor's Closest Comps So with a method to test this, i put Connor McDavid's numbers into the sheet and it spit out his closest comparables. Here are the top 10 forwards comparable to McDavid's 17-18 Season. (The smaller the "similarity score" the better.) His own season is obviously perfectly comparable with itself, but maybe people are on to something. Connor McDavid's closest comparable last year was actually Auston Matthews. The problem is that not all closest comparables are equal. Matthews and McDavid differ by a score of about 1. This likely means nothing to anyone, so I'll show you on a line graph. Matthews was technically McDavid's closest comparable, but McDavid is playing one game, and everyone else is playing another. However, if you look at Prospect Cohort analysis you will find that it is usually harder to find comparables for top tier players, and this is true to an exent. More pedestrian players do have much stronger comparables, but even other elite ones aren't nearly as far away from the pack as McDavid. To illustrate this, we'll do the same thing for Matthews, and to give him his best shot at looking one of a kind, I'll use his 17-18 season too, which was his best so far. If you look closely, you'll notice the scale here is much smaller. Matthews closest comparable is the ghost of his new teammate, John Tavares with a collection of all stars filling out the top ten, but no McDavid. Looking at it through Matthews' lens, there 33 players seasons more comparable to him than McDavid was last year. In fact Matthews was more similar to Marchessault than McDavid last year, despite the fact Matthews is technically McDavid's best comparable. For those who like the scatter plot view, here is the same thing but for Matthews, with McDavid highlighted. As you can see, relative to McDavid's plot, there are a much larger group of players, who are much more comparable to Matthews than anyone is to McDavid. So please, stop comparing players to McDavid. You doing a disservice to the player by doing so. They are probably special in their own way, but there simply aren't any players like McDavid in today's NHL, and barring some drastic change, there probably won't be for a while.
1 Comment
|
AuthorChace- Shooters Shoot Archives
November 2021
Categories |

 RSS Feed
RSS Feed
